[혼자 공부하는 머신러닝+딥러닝] 책의 내용을 정리한 글 입니다.
개념
다중 분류
: 타깃 데이터에 2개 이상의 클래스가 포함된 문제
로지스틱 회귀
: 선형 방정식을 사용한 분류 알고리즘
- 선형 회귀와 달리 시그모이드 함수나 소프트맥스 함수를 사용하여 클래스 확률(0~1 사이 값)을 출력할 수 있다.
- 클래스 확률이 1에 가까울 수록 양성 클래스, 0에 가까울수록 음성 클래스라고 판단 (딱 0.5는 음성 클래스로 판단)
- 이진 분류 - 시그모이드 함수 사용
- 선형 방정식의 출력을 0과 1 사이의 값으로 압축하여 이진 분류를 위해 사용한다.
- z가 무한하게 큰 음수 일 경우 0에 가까워지고, 무한하게 큰 양수일 경우는 1에 가까워진다.
- 지수가 음수인 경우 지수의 부호가 양수인 거듭제곱의 역수와 같다. x^-n = 1 / x^n


-
- 다중 분류 - 소프트맥스 함수 사용
- 다중 분류에서 여러 선형 방정식의 출력 결과를 정규화하여 합이 1이 되도록 만든다.
- 지수 함수를 사용하기 때문에 정규화된 지수 함수라고도 부른다.
- 다중 분류 - 소프트맥스 함수 사용

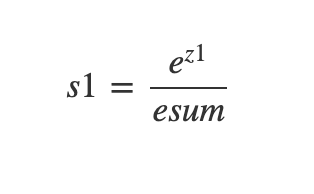
코드 작성
k- 최근접 이웃 분류기와 로직스틱 회귀 를 사용하여 확률을 구해보자.
데이터 준비
print(pd.unique(fish['Species']))
# => ['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']
fish_input = fish[['Weight','Length','Diagonal','Height','Width']].to_numpy()
fish_target = fish['Species'].to_numpy()
# 훈련 세트와 테스트 세트 분리
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
fish_input, fish_target, random_state=42)
from sklearn.preprocessing import StandardScaler
# 표준화 전처리
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv_data')
# 처음 5개 행 출력
fish.head()
print(pd.unique(fish['Species']))
# => ['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']
fish_input = fish[['Weight','Length','Diagonal','Height','Width']].to_numpy()
fish_target = fish['Species'].to_numpy()
# 훈련 세트와 테스트 세트 분리
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
fish_input, fish_target, random_state=42)
from sklearn.preprocessing import StandardScaler
# 표준화 전처리
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)k-최근접 이웃 분류기로 확률 예측
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier(n_neighbors=3)
kn.fit(train_scaled, train_target)
print(kn.score(train_scaled, train_target))
print(kn.score(test_scaled, test_target))
# => 0.8907563025210085
# => 0.85
# 타깃값을 전달하면 순서가 자동으로 알파벳 순으로 매겨진다.
print(kn.classes_)
# => ['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
# 모델이 예측한 처음 5개의 타깃값과 확률 확인
print(kn.predict(test_scaled[:5]))
# => ['Perch' 'Smelt' 'Pike' 'Perch' 'Perch']
import numpy as np
# 클래스 별 확률값 반환
proba = kn.predict_proba(test_scaled[:5])
# 소수점 네 번째 자리까지 표기
print(np.round(proba, decimals=4))
"""
=> [[0. 0. 1. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 1. 0. ]
[0. 0. 0. 1. 0. 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]]
"""로지스틱 회귀로 이진 분류 수행
# True, False값을 전달하여 행을 선택할 수 있는 불리언 인덱싱을 통해 도미와 빙어의 행만 골라낸다.
bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt)
# 처음 5개 샘플 타깃 예측
print(lr.predict(train_bream_smelt[:5]))
# => ['Bream' 'Smelt' 'Bream' 'Bream' 'Bream']
# 처음 5개 샘플에 대한 확률
print(lr.predict_proba(train_bream_smelt[:5]))
"""
=> [[0.99759855 0.00240145]
[0.02735183 0.97264817]
[0.99486072 0.00513928]
[0.98584202 0.01415798]
[0.99767269 0.00232731]]
"""훈련한 이진 분류 로지스틱 회귀 모델로 직접 확률 출력하여 비교해보기
# 로지스틱 회귀가 학습한 계수
print(lr.coef_, lr.intercept_)
# => [[-0.4037798 -0.57620209 -0.66280298 -1.01290277 -0.73168947]] [-2.16155132]
# 처음 5개 샘플의 z값 출력
decisions = lr.decision_function(train_bream_smelt[:5])
print(decisions)
# => [-6.02927744 3.57123907 -5.26568906 -4.24321775 -6.0607117 ]
# 시그모이드 함수에 통과시켜 확률 출력
from scipy.special import expit
print(expit(decisions))
# => [0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]
로지스틱 회귀로 다중 분류 수행
lr = LogisticRegression(C=20, max_iter=1000)
lr.fit(train_scaled, train_target)
print(lr.score(train_scaled, train_target))
print(lr.score(test_scaled, test_target))
# => 0.9327731092436975
# => 0.925
# 처음 5개 행 타깃 예측
print(lr.predict(test_scaled[:5]))
# => ['Perch' 'Smelt' 'Pike' 'Roach' 'Perch']
# 처음 5개 행의 예측 확률 출력
proba = lr.predict_proba(test_scaled[:5])
print(np.round(proba, decimals=3))
"""
=> [[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]
"""훈련한 다중 분류 로지스틱 회귀 모델로 직접 확률 출력하여 비교해보기
# 선형 방정식의 계수 확인
# 다중 분류는 클래스마다 z값을 계산
print(lr.coef_.shape, lr.intercept_.shape)
# => (7, 5) (7,)
decision = lr.decision_function(test_scaled[:5])
print(np.round(decision, decimals=2))
"""
=> [[ -6.5 1.03 5.16 -2.73 3.34 0.33 -0.63]
[-10.86 1.93 4.77 -2.4 2.98 7.84 -4.26]
[ -4.34 -6.23 3.17 6.49 2.36 2.42 -3.87]
[ -0.68 0.45 2.65 -1.19 3.26 -5.75 1.26]
[ -6.4 -1.99 5.82 -0.11 3.5 -0.11 -0.71]]
"""
# 처음 5개 샘플에 대한 z1~z7 값을 구한 후 소프트맥스 함수를 사용해 확률 출력
from scipy.special import softmax
proba = softmax(decision, axis=1)
print(np.round(proba, decimals=3))
"""
=> [[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]
"""이 장에서 사용된 핵심 패키지와 함수
scikit-learn
- LogisticRegression
- 선형 분류 알고리즘인 로지스틱 회귀를 위한 클래스
- predict_proba()
- 예측 확률을 반환
- 이중 분류 - 샘플마다 음성 클래스와 양성 클래스에 대한 확률 반환
- 다중 분류 - 샘플마다 모든 클래스에 대한 확률 반환
- decision_function()
- 모델이 학습한 선형 방정식의 출력 반환
- 이진 분류 - 양성 클래스의 확률이 반환 (이 값이 0보다 크면 양성, 작거나 같으면 음성)
- 다중 분류 - 각 클래스마다 선형 방정식을 계산 (가장 큰 값의 클래스가 예측 클래스)
'Machine Learning' 카테고리의 다른 글
| [혼자 공부하는 머신러닝+딥러닝] 결정 트리 (0) | 2023.05.09 |
|---|---|
| [혼자 공부하는 머신러닝+딥러닝] 확률적 경사 하강법 (0) | 2023.05.02 |
| [혼자 공부하는 머신러닝 + 딥러닝] 특성 공학과 규제 (0) | 2023.04.21 |
| [혼자 공부하는 머신러닝 + 딥러닝] 선형 회귀 (0) | 2023.04.15 |
| [혼자 공부하는 머신러닝 + 딥러닝] k-최근접 이웃 회귀 (0) | 2023.04.11 |



